Photobleaching is a common problem for light-sensitive organic molecules, which currently limits their use in optical devices. Some dye-doped polymers have been observed to self-heal after the dye molecules have been photodegraded. Very few dyes and polymer combinations are currently known to self heal from a photodegraded state and usually involve anthraquinone and rhodamines dyes doped in either poly(methyl methacrylate), polyurethane, poly(lactic acid)*, or glycol-modified poly(ethylene terephthalate)*. OOMG members are working towards creating a library of self-healing optical materials as well as uncovering the physical mechanisms of dye recovery in these systems.
Laser applications of self-healing dye/polymer systems are being investigated. We are currently developing an automated multilayer spin coater for in-house DFB laser fabrication, where alternating layers of self-healing materials are being introduced. OOMG researchers are also using coextruded polymer Bragg reflectors from CLiPS affiliates to fabricate and characterize self-healing DBR lasers.
* Discovered by OOMG undergraduate researchers
OOMG members are investigating a range of problems in nonlinear optics. Analytical solutions to sets of classical nonlinear optics equations can be obtained for only a few idealized scenarios. We are currently interested in analytical techniques to obtain generalized approximations to a broad class of problems in nonlinear optics.
From a quantum mechanical perspective, the nonlinear optical response of a charged system is limited by a relationship between a sum-over-states expression containing the transition moments. The transition moments are also constrained by the matrix elements of the Thomas-Reiche-Kuhn (TRK) sum rule. The TRK sum rule places an upper bound on the maximum linear and nonlinear optical responses a system can achieve, which are scale-invarient when the TRK sum rules are calculated from the Schrodinger equation. We are investigating how these boundaries scale under more generalized conditions such as relativistic scenarios or when the system can be described by the fractional Schrodinger equation.
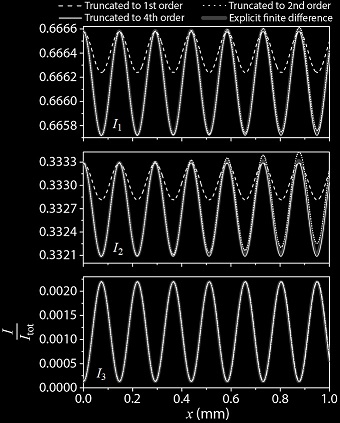
New techniques in perturbation theory are being researched to increase the tools we have to determine the optical response of molecules. The two most common techniques currently being used by researchers are finite-field methods or those derived from standard time-dependent perturbation theory (sum-over-states expression). We are developing methods to calculate the linear and nonlinear optical response through new perturbation methods with convergence out to higher orders. We are also applying homotopy analysis method to sets of nonlinear optical equations to determine analytical approximations with large regions of convergence.